我们常说的零和博弈zero-sum game，又称零和游戏或者零和赛局，是与非零和博弈相对的博弈论的概念。简单说，零和博弈表示所有博弈方的利益之和为零或一个常数，即一方有所得，其他方必有所失。在零和博弈中，博弈各方都不合作。在各种赌博和期货交易等等都很常见的。$ Z. ^# ^% d( g
★说起所谓【赌徒破产定理】要从在18世纪初，那群非常爱赌博的著名数学家说起。是他们提出了“赌徒破产定理”Gambler’s ruin。具体“一系列数学运算”，指在“公平”赌博中，任何一个持有限赌本的赌徒，只要长期赌下去必然有一天会输个精光。该定理1/2计算如下：( R: ` T6 k N4 B. n ^. n5 T
★假设对赌初始资金是n，每赌一次或输或赢，资金分别会变n-1和n+1。输或赢概率为 1/2一直赌下去。赌徒资金变为0概率多少？% |% o& p7 Y( c. z1 e
即从资金为n开始一直赌下去，n变为0的概率是P(n)： p(n) = (p(n + 1) + p(n - 1))/2，对n＞0.即数n有一半的机会变成n+1，一半的机会变成n-1。当 n = 0 的时候，即使不用赌，赌资也等于全部输光了，所以 p(0) = 1。
/ P) S1 A6 j7 Y% e4 p由此就可看作一个满足下列递推关系的数列：
4 A9 f( D# I9 W+ [( a+ kp(0) = 1+ k4 y! Z3 X8 p# Z7 V$ ]3 Q& C% I
p(n+1) = 2 * p(n) - p(n-1)- T0 m, c6 {3 _4 t9 p# u
设p(1)的值为a, 那么显然0< a<=1。利用p(n+1) = 2 * p(n)-p(n-1)，得：0 a3 ^4 U# Q/ f g
p(1) = a
% D' |3 y" e% f1 `5 U0 _ O1 Op(2) = 2a - 1
: k0 w1 ~) d0 |5 a9 C- {/ Cp(3) = 2(2a-1) - a = 3a - 29 Z: I" z- b. K$ R6 }
p(4) = 4a - 3 …… ……
/ d) [5 p& `8 V; D' {p(n) = na - n + 1.
3 Z" ^5 C: a' m+ U$ {% _/ E* q9 j我们知道p(n) >= 0对于任意的n成立。8 w+ @# Y! [0 p: Q
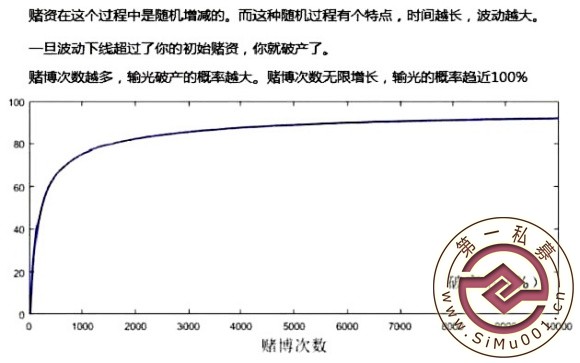
在n(a-1)+1这种情况下，a无限接近1，所以我们证明了p(1) 约等于 1. 同样的过程可以得到p(2)约等于 1,，… …，一直下去，p(n) 约等于 1，也就是赌徒资金变为0的概率为1(100%)！1 O; J3 z d' \5 u
…★其实这是违背大部分人的直觉结论：简单说，无论多富有，只要财富是有限的，只要在50%概率赌下去，必然会在某一次赌博中输个精光。其实如赌徒的财产作为状态，破产状态就像无尽深渊，是无法跳出来的。长期赌博的赌徒，总有一次会遇到连败“陷阱”状态。总有赌本已不可能再翻身的一天。' U' D/ e& T+ K. ~5 q' i5 r! O4 @
细想想，在任何类似开大开小的博弈局中(尤其期货交易最突出)，其资金曲线图就等于是操作者财运结果图表。这就像猜大小的运气一样，谁没有过某段时间事事不如意时？零和的期货市场就是用各种“无常”造出价格走势图。能在零和市场长期自如就需有极高心理素质。- Q8 C) Y8 X- b/ m. i
★所以真能长时间在期货能成功者，会发现都是风险厌恶型的冷血动物，都会像守在各自水域地盘等食物的泥水中鳄鱼，都在等自己看得懂的利益扑食。有些人也会疑问“韭菜”(当下的流行语)们会不会进入鳄鱼池呢？都在变聪明中，真的没有韭菜，发展出来的高手或主力就没了经济来源？但韭菜会消失吗？不会，因为市场大幅波动，会有人依旧进入前赴后继的寻找挣大钱机会。中国期货历年统计数据看，大致都是全年参与交易者的1/4会永远离开这市场，重新再换新鲜血液了。参与者需想开些，量力而行！即使公开期货私募也一样情况。
8 Y" r. i5 `8 J @ |
, ~% s! l! `4 v9 W$ h8 P' Y1 U5 l1 C0 \3 L
| 
|手机版|Archiver|
( 桂ICP备12001440号-3 )|网站地图
发表于 2020-5-4 08:43:28