
?( J& b0 ~' X K. `& @查尔斯·庞兹/ w, ?# K u" k" Q* m
由于铁汇的文章在网络上不测走红,有大量的人找到我,问了我不少关于某某某公司,某某某理产业物是不是骗局这类的标题。很遗憾的是,险些全部来问我的朋侪都遭碰到了差别程度的骗局,有的骗局涉案金额高达十几亿美元。故意思的是,骗局险些清一色都是各种变种的旁氏骗局。1 E8 n' j/ q1 e, Y& h7 y
所谓旁氏骗局指的是,做局人给受骗者以高利钱的答应,但是究竟上并没有任何增值的项目,纯粹是拿厥后者的投资款来付出之前受骗者的利钱。
; s; m* _3 C8 ^9 f比方,一个做局者声称1个月能给投资者带来10%的回报。第一个受骗者投资了100万,而做局者并没有投资任何一个项目。比及下个月的时间,他拿第二个月新来的投资者付出的钱中抽取10万给第一个投资者。. y+ ~0 q" T$ W# v2 V- H+ w' r0 t
 " F& t0 \% D* }) O$ z2 H " F& t0 \% D* }) O$ z2 H
3 D! c( E0 B$ K/ z; F% x& ~

) ~7 J- B( R* a" `) k3 j
e& l6 E3 M! X2 [5 j% H第一个投资者获取利钱纯粹来自于其他的新到场的投资者的投资款子,但第一个投资人确实拿到了利钱,而且倾向于信托投资项目的真实性。当一连数个月受骗者拿到了答应的高额利钱后,开始呼朋唤友到场这等“发财”的行列。如许旁氏骗局得以维系下去。
; a% x+ _1 y4 E# Z固然,我们知道没有真正的赠值项目作为支持,如许的骗局终会有竣事的一天。
( P( {0 t: Q2 B5 }- j8 g$ o0 J! f那怎样辨别一个投资项目,是不是旁氏骗局呢?; T5 I& G5 E" A- |9 v
实在,最最显着的特性就是不正常的高利钱。
! y% E7 p9 Y z c5 h* h- C# T大概你以为一个月10%的利钱不算高,我来讲个小故事。9 K7 A4 F- G9 ?( g0 B# W! B: H% J! \+ c
传说西塔发明确国际象棋而使国王非常高兴,他决定要重赏西塔,西塔说:“我不要你的重赏 ,陛下,只要你在我的棋盘上赏一些麦子就行了。在棋盘的第1个格子里放1粒,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,依此类推,以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放满第64个格子就行了”。戋戋小数,几粒麦子,这有何难,“来人”,国王令人如数付给西塔。 ( u: r$ y% \, Q& Y) h8 B- D5 o
% l6 J/ S. d" G8 a* v: j+ D5 l- D
计数麦粒的工作开始了,第一格内放1粒,第二格内放2粒第三格内放2’粒,…还没有到第二十格,一袋麦子已经空了。一袋又一袋的麦子被扛到国王眼前来。但是,麦粒数一格接一格飞快增长着,国王很快就看出,即便拿出天下的粮食,也兑现不了他对西塔的信誉。 6 k1 `, z2 x5 C0 M
1 Y" h/ ~' v X G. W- u* ~5 [6 ]
原来,所需麦粒总数为: =18446744073709551615
- W& X0 _% N: H
4 x& ^; T4 j9 O这些麦子究竟有多少?约莫820亿吨。按照如今环球大麦产量来看,大概550年才气满足3 \8 r0 k; M' }% X7 d3 m8 F6 K
这就是复利所带来的古迹,爱因斯坦曾经惊叹到:“复利是人类最巨大的发明,是宇宙间最强大的气力,是天下第八大古迹。”
( o' u5 o9 M5 j8 o" `8 ~3 b大概各人以为10%的月回报不算高,看下图* R8 T# E, Q4 c' z6 U) k6 s$ [: v
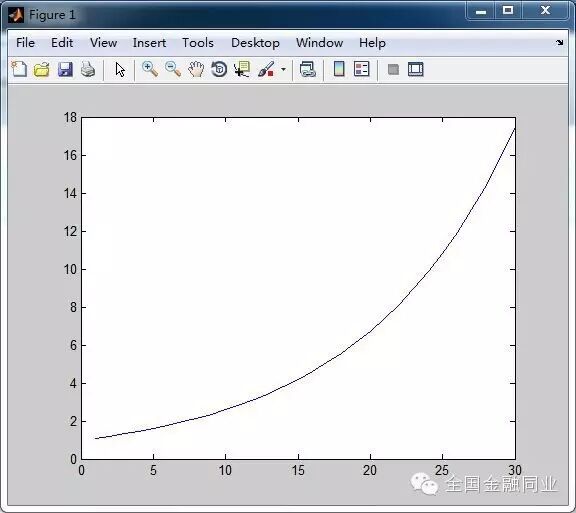
+ F% w* P: Z* v' ?" ^5 l& ] Y. Q% q I这就是如果有10%的回报率,财产增长的速率,末了是会一炮冲天的。如果10%的月回报是真实的话,那第二年,也就是第24次复利将会是9.8,靠近10倍。
8 x2 U5 B( X) s- [0 X而仅仅再过半年,到第30个月,就是17.44倍。满3年的时间,就是31倍。- {: F4 E( f, {. L
. y0 [- t2 z% |1 V, i. m* W- q7 E; B
你如果投资100万的话,3年后就应该给你3100万的回报。
: t4 Q, T; m3 x5 x) ~5 } : f# C$ u; s# F% a0 Q o
如果你筹划留遗产给你的子孙,10%的月回报率,放个20年给你刚刚走上工作岗位的子女,让他们不消辛劳为了钱做不喜欢的工作,可以自由选择奇迹的话。
& ~& I X) @5 X% T0 ]( p
; G8 p+ {3 W% x& z( F6 _& W/ v你如今投资1万元,240个月后是86亿倍的回报,也就是86万亿的财产,数量相当于客岁美国的GDP总量。你才投入1万元哦!9 u0 Y: Y* `2 J' |3 u
说到这里,各人应该明确了,10%的月回报的投资时机是不会主动找上你的。
; s0 k, q# B k# u+ q4 R7 o: P. s
+ e2 o% Q2 [' y天下上确实存在月回报10%的投资时机,但容量会有上限,由于市场有打击资本。也就是说,如果用同一个计谋的人多了,则该计谋必要购买的资产同时就会有代价颠簸,从而无法再以计谋必要的代价购买到。- V3 m! Y- a* a/ g) o5 F3 P
' Q. g5 R* U, I2 {/ Y
华尔街的对冲基金们,20%以上的年化回报率就已经富足交差了。由于对于土豪们而言,大量的产业增值的速率只会越来越慢,20%已经是飞速了。6 r# c& T! K- r; [5 L2 h& o: Q
# n# M+ a$ g3 b说到这里,已经很清晰了。如果有人答应你10%以致更高的月息,内心就应该知道怎么回变乱了。 v) [: f4 I3 [% n" q% Z
再再再次告诫各人:天上不会掉馅饼。& l y: t% j, o, B0 j; r2 F
旁氏骗局的特性是云云的显着,但屡试不爽。旁氏骗局会完蛋确实毋庸置疑,让我感爱好的是旁氏骗局什么时间会发展到高潮,什么时间幻灭?
) F$ [8 M0 A0 G7 y
/ U, i, T: }) s9 t* |& H话说这两天看到诺贝尔奖得主罗伯特席勒传授从前的论文,他曾在多次股灾前正确得预言了股灾的肯定性。用的就是旁氏骗局来类比股市。
7 g8 E3 B% a4 Y- n' r7 v! J
5 X7 i" A0 F0 L. I t c看来研究旁氏骗局不光有戳穿骗局的功效,还能应用于金融证券谋利的学问上。
6 A+ z. u, u( J0 u8 u% N7 Y索罗斯在他的著作中,提出了“反身性”的模子,以颠覆传统的经济学表明。而罗伯特席勒传授则用举动学的观点来指出传统经济学模子的缺陷。 l$ m4 |, Y# ^, s8 `2 E

' j6 s- Z4 [$ M索罗斯给出的模子提出了两个离经叛道的观点。
' S+ b3 J& o C& u& s4 b) l: p0 c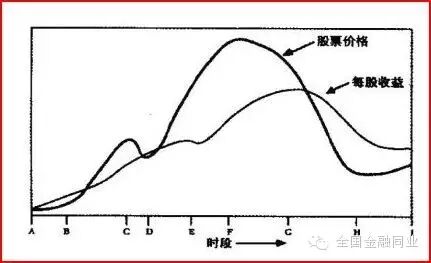
, E) G/ a7 E M/ A股票的代价并非围绕股票的代价而颠簸,而是具有“反身性”。即已往代价的提拔带来升值预期,故而新进入的投资者会买入持有。
/ N3 r* {- h) I
1 L4 W7 c; c+ w* z. g7 N F买入持有者并不是看好每股收益而购入,而是他们预期股价会继承上涨,可以卖给厥后的投资者。
$ W. s) Z& N0 S8 G8 `" X
2 R* w$ Z: e* S固然股票的代价有升值空间,但谋利者在这里预期的变乱和庞氏骗局是差不多的。即,我所盼望的收益是厥后的到场者给出的。! E* [( e+ i+ Y) |
3 ]1 a& }9 b& W
全部的人都渴望着厥后的到场者到场进来,但到场者的上限,大概说到场者的资金上限并不是无穷的。 Z( \1 U9 w2 X6 S4 ]$ {, t* E$ i1 i3 l
1 V5 M7 w% L& j% u" z& b
这导致整个过程肯定面对和旁氏骗局一样的结果——泡沫的幻灭。
. `3 {9 g# {+ M! t- v - ?& [- O3 R' t6 N: N
差别的是股票究竟是有代价的,而一样平常的庞氏骗局背后没有任何有实际代价的东西。也就是说,当股价一起降落的时间,一样会产生正反馈效应,厥后的做空者会预期代价更加低,以是更加卖出。而前期的谋利者会产生类似踩踏变乱中的情况。' n( g& y1 Z/ I6 i+ x' c
7 b$ i9 Q0 ^0 c' Z3 P
一旦股价下跌到,光持有股票,得到的股息也是一笔不错的投资时。套利者就会出现,大概我们可以叫他们“代价投资者”。光持有这些便宜的股票,赚取股息即可得到不错的回报率。# k9 n- ^, P. w' X. l; r5 s
, a0 p! e, h4 R! a
这是第一个离经叛道的观点,不围绕代价简单颠簸,投资者自己的举动自己是影响未来代价的因素。+ y; M/ k2 F: x4 A8 e
第二个离经叛道的观点是,今世价被谋利者推高的时间,该上市公司的融资源事会增强而导致原来的代价提拔。买股票的人多了,这公司的融资源事会资助其扩展业务。# i7 R; P& v: R( _0 ?9 g% u- G. T
r+ T1 [* l0 u% i降落的时间,会有类似银行挤兑的征象。原来根本面良好的公司大概由于惨烈的股价下跌而遭受丧失,造成该公司的代价受损。
( c; v/ K' ^0 g) c# q2 J/ [观察者自己会影响被观察到事物,而非经典模子的观察者无关。
6 m# I/ R$ I6 W6 f$ i/ Y & C: B6 H6 S8 B, ^0 T
我们这里界说一下广义的旁氏骗局:谋利者都渴望厥后谋利者的新入资金推高而产生收益,而非看好该资产自己能产生的代价。
( K* }1 y# p1 G) ?3 I # G4 U3 L& a% B1 b* ^
简单搜刮了一下,并没有找到好的旁氏骗局的数学模子,由于爱好(闲得蛋疼),和两个同事简单搞了一下。" o* H% \9 G2 l1 l Q+ \# x
旁氏骗局的每次入金函数界说为 I(n)
4 ]* G$ {% B7 g, ]$ l$ Hn 为到场的次数
! ]/ W% e" D( e- P, }% T3 t6 \8 RO(n) 函数为出金的函数,而出金的数量和入金的比值,称为该月出金意愿,用函数P(n)来体现。
" K4 ?) N% t2 u! k# I' g+ O$ `! B5 ]而出金包罗本金和利钱,回报率设置为固定的 r
. h% `9 c: t8 N. Q6 ~1 Q/ L$ s* i则做局者当月现金流 N(n)=I(n)-O(n)
' g5 ^, f/ ?, L6 WN(n)=I(n)-O(n)=I(n)-[P(n)*N(n-1)+N(n-1)*r]
& ~( d8 d3 _5 C3 k! j ( x* m, B, b) J& g2 \8 u3 e
是个递归的式子。标题是我们没办法获取到入金的数据和出金的意愿。而旁氏骗局做局者的账本也获取不到。(谁操盘过旁氏骗局可以悄悄给我个账本,我包管不举报你 :P)( ?: ~8 K& y" k2 {1 d$ S8 ~
5 g6 b8 u1 Q5 g* d无奈,只有模仿一下了。回顾旁氏骗局的过程,都是惊人得相似。一开始投资者会非常审慎得小小实行一下。比及实行3次都乐成后 ,就会变得疯狂起来。
; {% H( ]. j- X- X8 G
7 O5 W; h6 y& n* h4 b5 V3 R借助杠杆是不可拦截的变乱。但全部人借助杠杆都是有上限的。故而我们用正态分布做假设搞了个模仿的样子。
$ ~+ M$ y7 A" \syms x;f1=exp(-((x-10)/5)^2);s1=int(f1,x);s1=simple(s1)/ b# X( g# D' Y! M' M
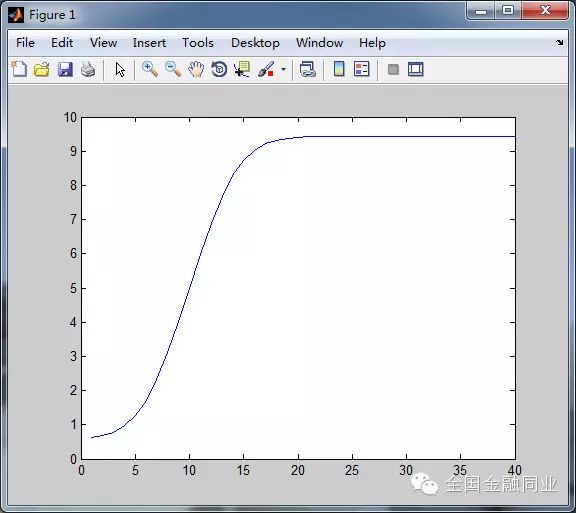
4 C y$ h! F8 h* c3 @+ {7 v% U这根曲线的意思是,一开始的入金是比力迟钝增长的,实践乐成5次左右,就会飞速增长入金,然后到达杠杆的最大限度,开始收敛。
+ A4 p: `" P& T" B z - Z+ J% P. i- F) d4 y6 i! W
而出金的意愿也是和融资源事干系的,出金的意愿在一开始实行的时间是比力强的。实行旁氏骗局第一次乐成后,会要求出金,试试是不是真的赚到钱。9 o4 K" ~/ i. q
/ H) ~6 y- ~0 x( F- O而实行乐成多次后,就会要求利滚利,不会要求快速出金,直到融资的本领碰到上限。被迫进步出金意愿。5 B4 _0 w V* I" }9 {$ F6 J2 W# W
由于必须兑付一部分利润给融资的泉源方。
/ |: p, X3 V" T& B2 S/ SP=(x-10)^2/500;er3 _( f& k% b! g2 n7 D6 `& D0 \
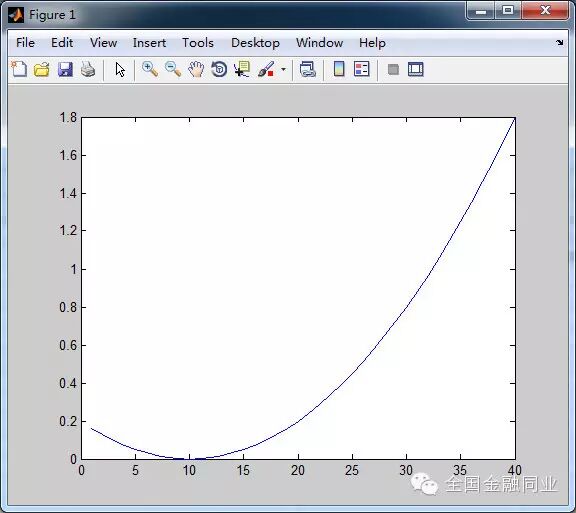
! a2 I) j' L( b上面这图就是出金意愿的曲线图,到实践到第10次左右,是不愿意出金的。
% ~; l8 {7 u6 M) }末了,我们用N(n)来模仿每个月做局者的现金流入,是一个递归函数,每次都是以上一次的入金和受骗者自身的情况而定的。, k3 l' m3 b* u$ E2 e7 [. C
O(1)=0;I(1)=(5*pi^(1/2)*erf(1/5 - 2))/2+5;N(1)=I(1) (1)=(1-10)^2/500;for i=2:40 MO=((5*pi^(1/2)*erf((i-1)/5 - 2))/2+5-O(1))*(0.1+(i-1-10)^2/500); O(i)=MO; I(i)=(5*pi^(1/2)*erf(i/5 -2))/2+5; P(i)=(i-10)^2/500; N(i)=I(i)+(0.9+P(i-1))*(I(i-1)-O(i-1));end (1)=(1-10)^2/500;for i=2:40 MO=((5*pi^(1/2)*erf((i-1)/5 - 2))/2+5-O(1))*(0.1+(i-1-10)^2/500); O(i)=MO; I(i)=(5*pi^(1/2)*erf(i/5 -2))/2+5; P(i)=(i-10)^2/500; N(i)=I(i)+(0.9+P(i-1))*(I(i-1)-O(i-1));end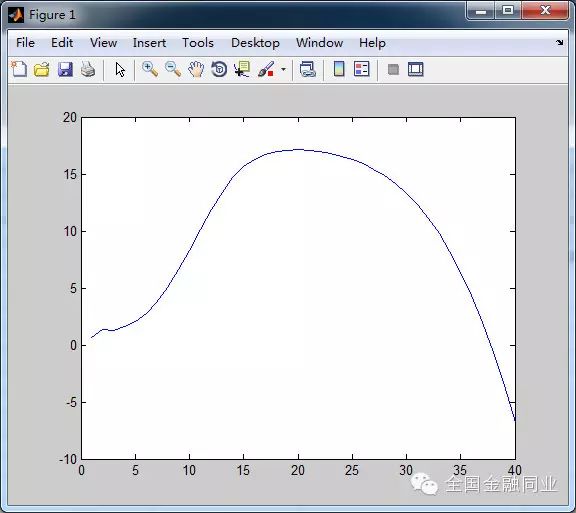 ; P) y. ]. I& `# l3 h5 Y ; P) y. ]. I& `# l3 h5 Y
上面这张图是做局者每次的净收入,旁氏骗局一开始的净收入在出现短暂的下滑(根本都是新入者,故而会有大量的牛刀小试),之后就会产生快速得增长。' `8 f3 a- s# M9 Y+ G3 c) u
$ ?5 j' \& a+ z' {' v N% Z我们这里设置的是10%的每次回报,出金意愿和入金速率都是模仿出来的,没什么依据,完满是为了符合我的直觉感受。
6 Y' ~3 K) s: [, J2 U7 [
# D" u- h! [1 O如许的模子实行到第18次左右碰到拐点,这个时间做局者可以感受到收入增长的速率为零。出金的压力开始陡增。(附带插一句,铁汇开始赠金模式之后18个月开始100%增金,疯狂加大了力度。而每次的套利收益大概在10%左右,我们的假设模仿出的效果,非常契合。思量到铁汇有大量的营销资本,故而出现资金压力应该早于第18个月)
" k- f: \% V( U5 T- F$ p % A, D/ o3 ^* N7 s; e1 m& e
之后是承付利钱的复利式增长,从而使得做局者收入的增长速率急剧淘汰。当实践到第36到37次左右,开始出现负增长,即本月做局者无利可图。
`2 A3 C7 P3 f ]6 e6 ~ 9 t- F2 g( ^! v) P- L5 B. I: i4 l+ M$ E
究竟上,做局者并不必要比及酿成亏本交易才脱离。当时间到18次左右,就可以开始摒挡金饰了,转移资金还必要点时间。那么比及大概第31,32次左右的时间已经根本完成了。
& `$ F7 O- |/ |2 X" v' v) w( O- t 7 ?# z( N9 `. B5 A/ r$ ~: n
可以看到,旁氏骗局的模子是不对称的。上涨的速率是比不上下跌的速率的,而且会跌破初值。
* |) ?9 _) c7 A7 s; p. Q
% W5 O; e( ]0 E) p+ r! ?* L这么一种不绝迭代得递归下去,如果没有内在代价的支持,比如纯粹的旁氏骗局,就是一个一文不值的东西。
& {$ r/ g. u0 _$ x: C7 t这张图很故意思,我们再看看索罗斯给出的资产代价的模子:
5 @! I8 s( [5 G4 ?" w' ~
% O; R" T# H3 ]8 o如果索罗斯是对的,资产代价的攀升是相互影响的,而且是类似旁氏骗局的期待下家接盘的情形,那么泡沫幻灭后的降落速率会显着快于上涨的速率。: ], d5 [3 x& h$ R1 w
* N% `% `' `5 @1 b( [ T0 W
涨是逐步涨,而跌是一下子发作的股灾。背后还是复利模子的原理。
~7 ~/ a# z/ f: {# I# H' E
* ^3 N; w! g) o" F% x那我们再反观有代价的资产最低点的形成,当资产的代价已经使得持有产生的股息和股价相比变得非常划算,那买入这个资产将是一个类似套利的时机。
( \! m0 P- I s ) N4 g# t4 ?& F9 y3 g
就算资产跌到0附近,也是不消恐惊的。
0 a' V& h# J7 H% c N! {0 Q7 u8 C & x. H2 b2 F/ `- V7 F
而只要如许的变乱发生,对于看重股息的投资者而言,就是千载一时的时机。而且如许的时机一但出现频频,我们又可以用到复利的神奇魔力。
8 j c" `# Z& ^* N, t" Y) t N 6 C4 _/ x0 Y7 _6 _; y! @7 ?2 F
只要股灾发生多少次,则复利会把我们推上天下首富的位置。
9 j4 H2 U8 A, u9 k - l* I9 |( @ `
这次复利的模子真的发生威力了,我想各人应该想到了同一个人。$ g6 J2 j/ J3 d' n( r0 T
 8 B; f! O# X9 G" Q 8 B; f! O# X9 G" Q
这种抄底计谋不必要思量什么时间旁氏骗局会崩盘,必要的是强大的估算本领,知道如今的代价买到的资产,是不是到了以后可以无视代价的程度。6 c' L2 U) l9 t; g, j3 |- x
, k* o& |! f* i1 i. R我比力关心的是,旁氏骗局,那种靠新来者付出老玩家利钱的模子什么时间会崩盘,有无先兆。0 n4 a2 _+ L2 y* ~! Q. `
既然杠杆是有上限的,而杠杆的上限导致我们的出金意愿被迫增强,函数P(n)的增长造成崩盘,那么至少有两种情况:2 C/ w$ ^1 L( u3 ?5 M
(一)融资源事到达上限,借不到更多的钱维系。那么只要看到场者的融资杠杆率开始降落即可知道拐点会到来。
! {! a5 W6 S9 a3 t(二)杠杆率被欺压低落,如果央行加息等因素导致融资的情况突然发生变革,则拐点将突然到来。. L+ {: i) {9 V7 t9 p
- g/ j5 O, M" F6 Z6 n如许表明为什么股灾前去往有央行的紧缩政策,大概能自作掩饰。
6 D+ b2 L! o, h
& j6 ~* R; G7 n固然,这个只是本日心血来潮,任意模仿的一个小模子。不大概真的表明机密的市场举动,也不能作为资产代价推测的模子来严肃对待。0 a$ [/ |2 a0 I6 @4 p* C4 w( u
1 ~' j9 s' N7 c/ H/ E4 u
各人只必要记取,远高于正常利率的投资”好时机“,会是个万劫不覆的大坑就好了。! O% X3 ~, O) g# ^) x" q% l8 Y
, R2 N1 j& }; J! p( q: B只要能包管不去企图不正常的高息,任何旁氏骗局都将对你无可怎样。 |
 |手机版|Archiver|
( 桂ICP备12001440号-3 )|网站地图
|手机版|Archiver|
( 桂ICP备12001440号-3 )|网站地图